Project Model S

Parallel Variational Shape Approximation for simplifying 3D scanned dense meshes

Proudly presented by
George Zhu and Min Park

Final Report - Project Model S

11 Dec 2017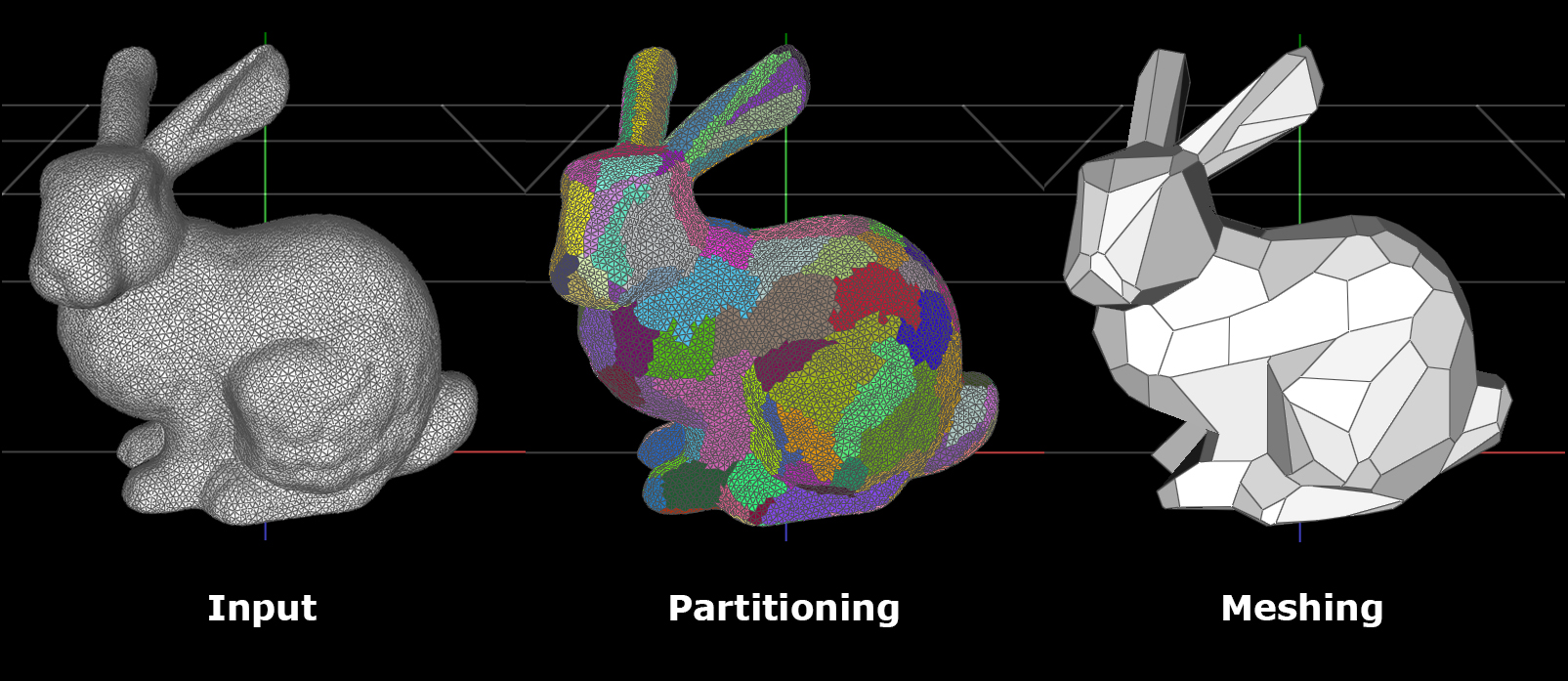
Summary: We implemented the sequential Variational Shape Approximation for simplifying large mesh from 3D scanners. We designed and implemented in CUDA two parallel approaches for distortion minimizing flooding, which is the most computation-intensive part of the algorithm, and achieved 7.28X speed up on GTX 1080. We also achieved a 22.31X speed up with GTX 1080 on the second most computation-intensive part.

ResultImg

Background: Sequential Algorithm Re-visit

As described in the paper by Cohen-Steiner et al., the Variational Shape Approximation algorithm for simplifying meshes consists of two major steps: partitioning and meshing. Given a mesh, VSA will first partition it into clusters and then generate a simplified mesh based on clustering results.

After preliminary testing, we found that the first part of the algorithm takes up more than 95% of total computation time. Therefore, we decided to focus on parallelizing the partitioning step.

Cohen-Steiner et al. proposed an efficient partitioning algorithm with O(NlogN) complexity for each iteration (where N is the total number of triangles in the mesh):

loop until converge or maximum iteration is hit:
    Flooding()
    Fitting()

where Flooding() and Fitting() are each defined as

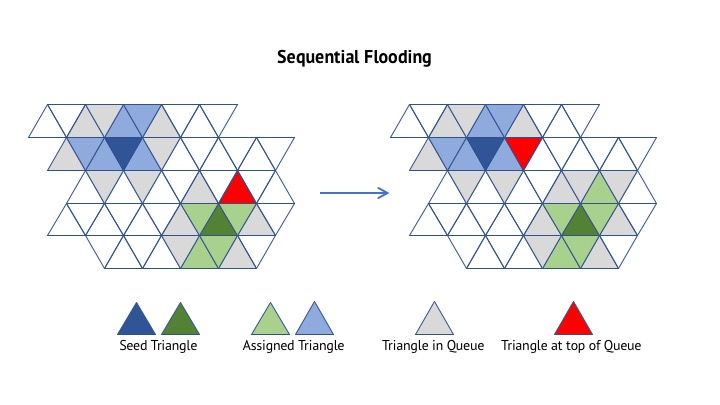
Flooding():
define P as the number of partitions(Regions) desired
define R as the array of P Regions
define Q as the global priority queue

initialize at random P seed triangles as Ri.seed on the mesh

for each seed triangle T:

    define i as the Region index T has been assigned to
    
    insert its three adjacent triangles Tj in Q, with a priority 
    equal to their respective distortion error 
    E(Tj,Ri) = ||Tj.normal - Ri.normal||

while Q is not empty:
    pop the triangle Tj with the least distortion error from Q
    if Tj has already been assigned to a Region:
        continue
    else:
        assign Tj with the Region index i
        add Tj's unlabeled neighbors (at most two) to Q

Fitting():
for each Ri in R:
    calculate area-weighted average normal of all Tj assigned with
    Region index i
    
    update Ri.normal
    
    for all Tj assigned with Region index i:
        find Tmin whose normal is closest with updated Ri.normal
        assign R[i].seed as Tj

diagram1

Two Parallel Flooding Approaches

From the sequential algorithm description, our observations are that:

  1. Fitting() is basically a data-parallel approach. Therefore parallelizing it is relatively simple: we just need to parallelize across the triangles to achieve good speed up.
  2. Flooding() is a more complicated case because of the involvement of a the global priority queue. We cannot expect the exact behavior as the sequential algorithm with a parallel approach. As a result, there are performance-accuracy trade offs in parallelizing this part of the algorithm.

We integrated CUDA in Scotty3D and implemented all our algorithms on top of it. We used the thrust library for its exclusive scan features. We got the inspiration of the two approaches from two papers that address similar problems, and designed our own parallel algorithm.

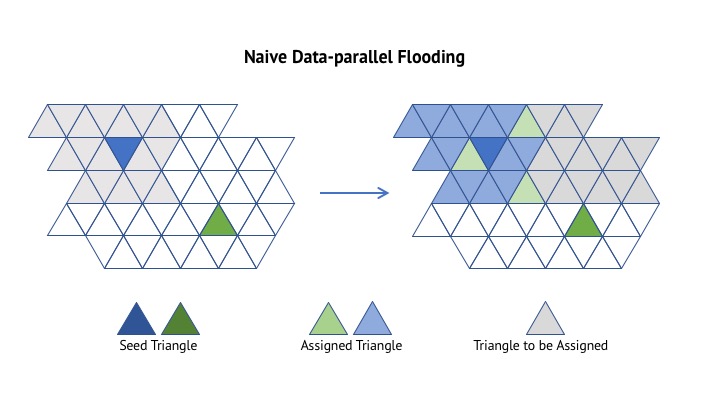
Naive Data-parallel Flooding

diagram2 (Inspired by Fan, Fengtao, et al. “Mesh clustering by approximating centroidal Voronoi tessellation.”)

define P as the number of partitions(Regions) desired
define R as the array of P Regions

initialize at random P seed triangles as Ri.seed on the mesh

parallel for each triangle Tj in mesh:
    for each Ri in all Regions:
        compute the euclidean distance (as approximation to 
        geodesic distance) of Tj.centroid and Ri.centroid
        
    pick the nearest M (we use 8) Regions of Tj and compute 
    E(Tj,Ri) = ||Tj.normal - Ri.normal||
    
    assign Tj with the Region index k where E(Tj,Rk) is the minimum
    among the M Regions

In this approach we eliminated the priority queue completely. We approximate its behavior by picking the nearest M regions around the triangle. Considering each iteration, this algorithm has total work of O(N * P), where N is the number of triangles in the mesh and P is the number of partitions(Regions) desired. Based on implementation above, the span of it is O(P).

After testing, we found that the accuracy of this approach is not satisfying and that too much additional work is introduced. So we moved on to a more sophisticated approach.

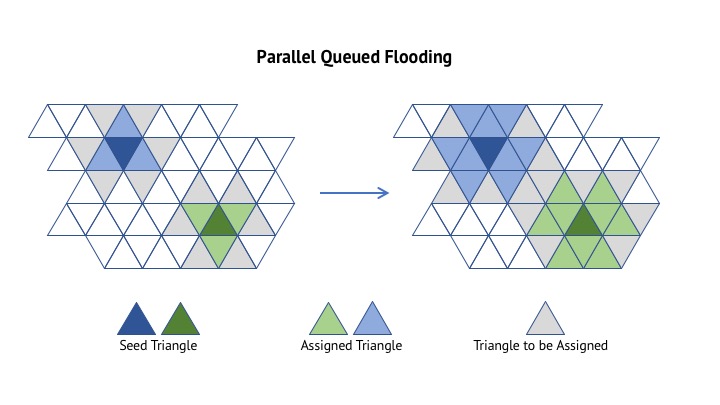
Parallel Queued Flooding

diagram3 (Inspired by Sébastien Valette et al. “Generic Remeshing of 3D Triangular Meshes with Metric-Dependent Discrete Voronoi Diagrams”)

define two queues Q1, Q2
define P as the number of partitions(Regions) desired
define R as the array of P Regions

initialize at random P seed triangles as Ri.seed on the mesh
add all P seed triangles to Q1

while Q1 is not empty:
    parallel for each triangle Tj in Q1:
        find the region assignment of Tj's three neighbors
        
        for each assignment Ri, calculate distortion error E(Tj,Ri)
        and choose Rk with the minimum E
        
        if Tj has not been assigned region or Rk is different 
        than previous assignment Rk':
            assign Tj with region Rk
            add all Tj's neighbors to Q2
        else:
            continue
    replace Q1 with Q2

Queue is implemented as follows:

1. allocate an output array and a indicator array, both of size 
   numTriangles+1, initialized to 0
2. when adding a triangle Tj to queue, mark indicator_array[j] as 1
3. exclusive scan on indicator_array, store result in an array scan_result
4. if indicator_array[j] == 1:
        output_array[scan_result[j]] = j;
5. output_array is now a queue of size scan_result[numTriangles]

In this approach, we are parallelizing across the regions. Each region will “grow” in parallel from its seed face. When the border of one grown region touches another, the two of them will “fight” to push the border in a distortion-minimizing direction until minimum distortion is achieved.

Because of the exclusive scan, the total expected work in each iteration is O(NlogN * sqrt(N/P)). Based on the implementation above, the expected span is O(logN * sqrt(N/P)), assuming exclusive scan has the span of O(logN).

Random-access Mesh Data Structure

Originally, Scotty3D used a pointer-based data structure to store the mesh. However, since our project involves parallelizing, we needed a way to access the data without pointer chasing since that would leave little to no room for paralleization. Therefore, we decided to store the data in a vector. This vector based data structure allows us to access random faces, without having to pointer chase, which is crucial for our parallelization algorithms.

We observed that for the sequential algorithm, using the random-access data structure will yield a 3X speed up compared to the pointer-based halfedge data structure. Therefore, for a more accurate assessment of the parallel algorithm, both sequential and parallel algorithm run on top of the Random-access Mesh Data Structure.

Parallel Speed Up

Test enviroment

We tested the sequential algorithm on a Intel® Core™ i7-6700 Processor (8M Cache, 4.00 GHz), and the parallel algorithm on 3 different GPUs:

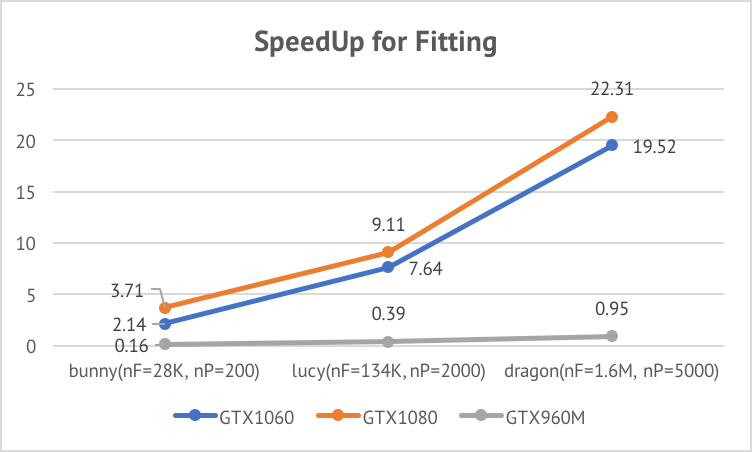
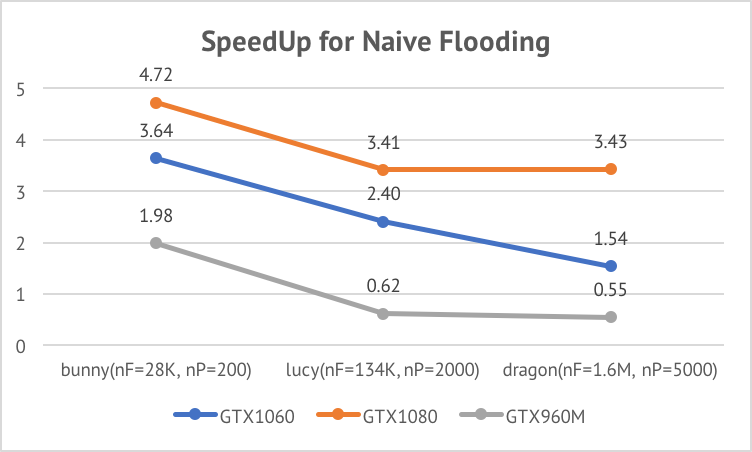
The speed up curves are listed below. 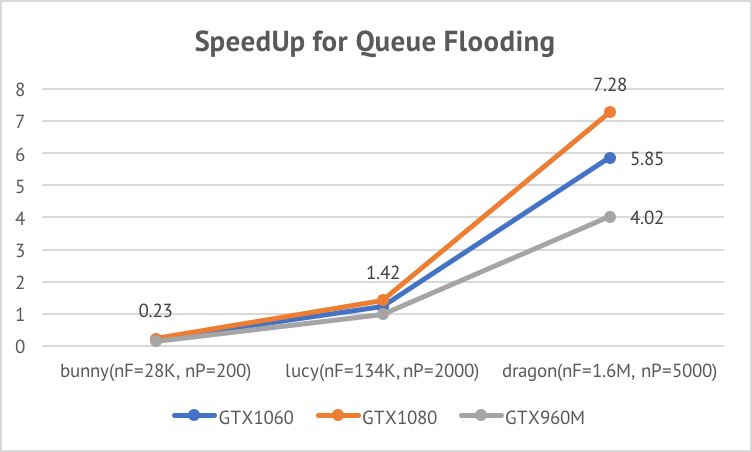Speedup1 Speedup2 Speedup3 Although Naive Data-parallel VSA achieved a near-linear speed up across GPUs, its speed up with repect to the sequential algorithm decreases as the size of input increases. This is be cause the algorithm has introduced addtional work that is linear with respect to P (number of desired partitions).

Parallel Queued VSA involves a queued flooding in lock step. Therefore it cannot achieve a linear speed up across different GPUs. Its speed up increases as the size of input increases. From the expression of the span of the algorithm, O(logN * sqrt(N/P)), we can see that the amount of parallelism will increase as P increases. In practice, for large input, P is often set to a larger value compared to small inputs. Therefore, Parallel Queued VSA is more suitable for simplifying large meshes.

Convergence Analysis

Based on Cohen-Steiner et al., the goal of the algorithm is to minimize total distortion error. So, both the value of the distortion error and how fast it will converge reflect the quality of the algorithm.

Shown below are the convergence curve we obtained on three different inputs.

Converge1 Converge2 Converge3

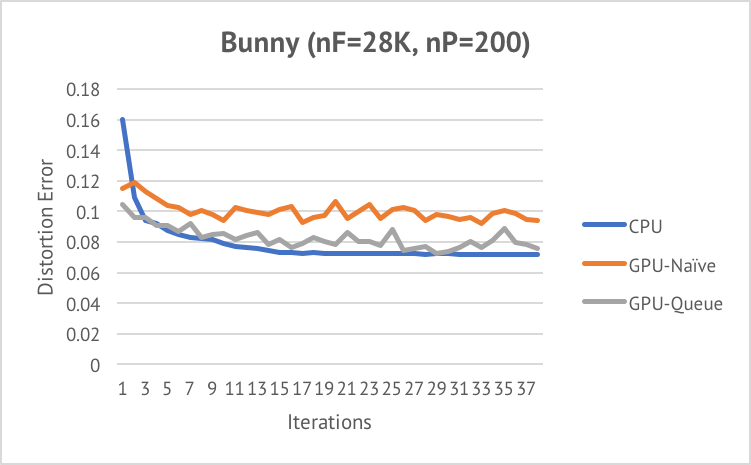
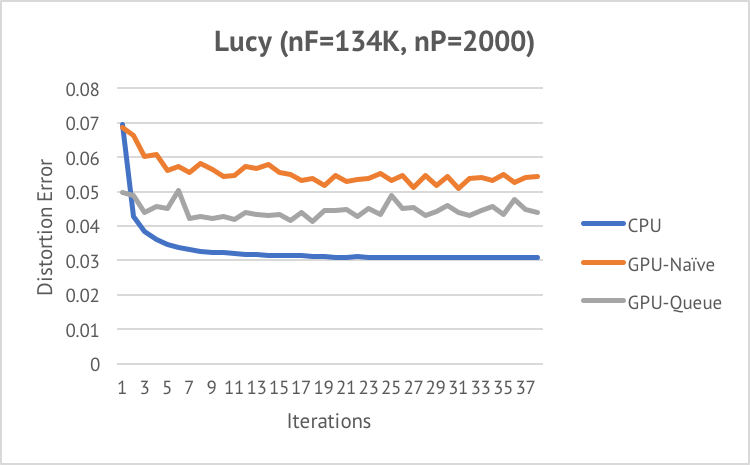
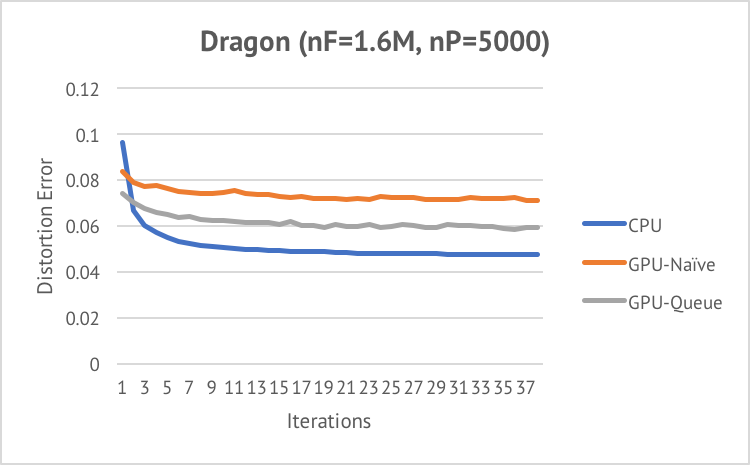
We can see that all three algorithms converge very fast in less than 10 iterations.

Queued VSA performs better than Naive VSA in terms of minimizing distortion error. Both parallel approaches are worse than the sequential algorithm. The reason is that although parallel flooding also tries to minimize distortion error, it does not guarantee the output regions are connected. In order to feed the output of the partitioning step to the meshing step, one iteration of sequential flooding is added after the parallel algorithm coverges. Therefore, to ensure connectivity, the value of distortion error is increased by the final iteration of sequential flooding.

Discussion

In general, the Parallel Queued VSA algorithm achieved satisfying speed up and output quality. However, to put this algorithm into practical use, more work should be done on both steps.

For the partitioning part of VSA, future work can focus on improving speed up (by utilizing optimization techniques such as shared memory) and improving output quality by solving the parallel connectivity problem.

More work should also be done on the meshing part. Current meshing algorithm doesn’t handle edge cases quite well. Many of the edge cases are not addressed in the paper by Cohen-Steiner et al. or any other paper/implementation.

References

Related Posts