More Backgrounds
Simplification vs Resampling
There are two major approaches to simplifying a mesh: simplification and resampling.
The simplification of dense 3D meshes has been a research question for a long time. It is basically a top-down method, where we start from a dense mesh and try to achieve simplicity by recursively removing vertices/edges/faces.
The general approach to this problem usually includes these steps:
- Assign priority to vertices/edges/faces to be deleted based on some error metric.
- Build a priority queue that tracks these vertices/edges/faces.
- Poll elements out of queue and delete/collapse them, resulting in a new mesh that has less faces than the previous one.

The metric used to determine priorities of simplification can be crucial to the final output. Many different approaches to calculating this metric were introduced. In 1997, Garland and Heckbert introduced Quadric Error Metrics, which has been widely used and improved upon. The basic idea can be described as follows:
Suppose we are collapsing an edge into a point P, the error is defined as (roughly) the sum of distances from P to all the original edges’ neighboring faces. For each edge, find an optimal point that this edge will collapse to, which minimizes the error (defined as the cost of this edge). Recursively collapse edges that has lowest cost. For many simplification algorithms, deletion of elements is local mesh manipulation, thus making it suitable for parallel optimization (Christopher G. Healey). However, it is very hard to directly control the output of simplification algorithms. These algorithms often focus on compression of an object for rendering purposes, such that the downgrading of visual effect falls within a tolerable range.
Resampling is another technique that can be described as a bottom-up method. Given a dense mesh, we try to sample it by building a simpler grid. This can either be achieved by building a uniform grid (W. Sweldens and P. Schroder) or some adaptive sampling method that either considering curvature (Alliez et al., Interactive geometry remeshing), or direction fields (Alliez et al., Anisotropic polygonal remeshing).
For human editing, remeshing by universal sampling and even adaptive sampling is not enough. The number of control points that is suitable for human adjustment is still far less than the output from the above resampling algorithms.
To combine the benefits of the two approaches, an error-driven remeshing technique is introduced. This approach amounts to generating a mesh that maximizes the trade-off between complexity and accuracy. The complexity is expressed in terms of the number of mesh elements, while the geometric accuracy is measured relative to the input mesh and according to a predefined distortion error measure. The efficiency of a mesh is qualified by the error per element ratio (the smaller, the better). One usually wants to minimize the approximation error for a given budget of elements, or conversely, minimize the number of elements for a given error tolerance.
Cohen-Steiner et al. proposed an error-driven clustering approach that does not resort to any estimation of differential quantities or any parameterization. Error driven remeshing is now cast as a variational partitioning problem where a set of planes (so-called proxies) are iteratively optimized using Lloyd’s heuristic to minimize a predefined approximation error.
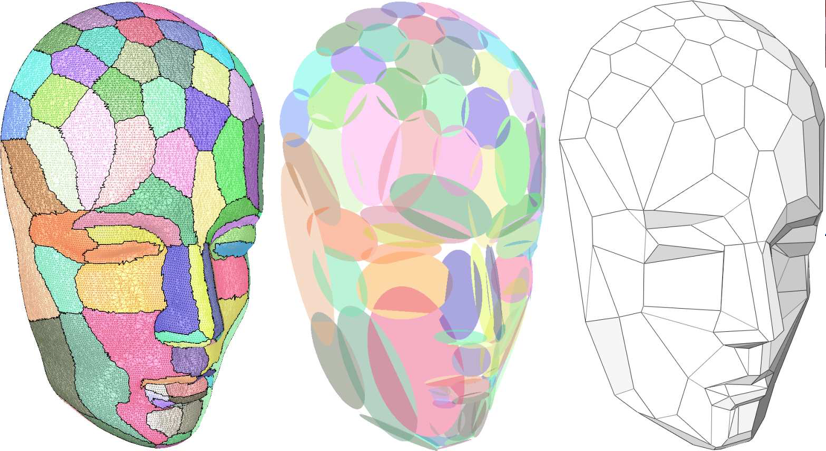
The method, Variational Shape Approximation, is beneficiary in the following ways:
- It outputs polygon mesh, which is user-friendly to human editors.
- It adheres to the geometric structure of the original object.
- It enables interactive remeshing. User can point to parts of the original mesh to add a face to the simplified result.
Although this method has many benefits, current implementations are mostly sequential and inefficient. Its suitability for processing 3D scanned meshes are untested. This brings about a potential opportunity of making the algorithm run efficiently, in order to support user interaction.